前回、奥行の推論の基礎編について解説した。
詳細については、前回のブログを参照して頂きたいが、数式や記号が羅列されており、わかりにくかったかもしれない。
後にも述べるが、奥行の推論の基礎編は、実際に経験した症例について、時系列を加味した上でより確からしい解釈を行うための方法であり、今から介入しようという症例についての臨床推論については役立てにくい。
そこで今回は、今から対応しようという方にとっても使える、奥行の推論応用編について解説していく。
題名にもあるが、重要な点は逆算思考力である。
それでは始めよう。
今までのおさらい
簡単にこれまでの縦の推論・横の推論・奥行の推論についてまとめてみる。
縦の推論
目の前の対象者にとある解決すべき現象(課題)があった場合、その現象について細かく検証し、原因について追及していく推論のことを指す。
基礎医学や臨床医学、バイオメカニズム的な前提にして、対象者の問題点と原因を階層的に結びつける形をとる。
ある現象を深めて考えていくことについては強く、それが妥当であった場合は、その後により高い介入効果を示すことができる。
一般的に言われている”現象と問題点の関係性”が異なるケースや、不確実性をはらんでいる現象の場合には、問題点と原因の関係性を誤認してしまうリスクが高い。
横の推論
目の前の対象者にとある解決すべき現象(課題)があった場合、同一対象者の他の現象と並列的に比較し、解決すべき現象の原因についての検証していく推論のことを指す。
様々な角度から課題の原因について追及できるため、現象と問題点が別の次元に存在する場合においてもミスリードされにくく、介入とすべき対象が大きくズレることを防げる。
ありとあらゆる情報を課題の原因追及に活かすことができる。
縦の推論ほど突き詰めて考えられるわけではないため、介入対象は大きく外しにくいが、ピントがぼやけている可能性が高く、介入効果として不十分になりやすい。
様々な情報から処理していく必要があるため、推論の質が療法士の情報処理能力に依存する。
奥行の推論
患者の時系列を含めた情報について、適切に整理し、判断するための方法を指す。
時系列の異なる情報について、比較検証できるように整理することで、より確からしい推論が可能となる。
あくまで情報の整理に主眼が置かれているため、最終的な推論については、他の推論を用いる必要がある。
前回の奥行の推論に関しての説明では、介入前後の比較など、対象者への介入の結果から対象者の問題点を整理して検討する方法として説明した。ただ、これでは自身の臨床における知見を増やすという意味では効果的だが、リアルタイムで介入している対象者の問題解決には繋がりにくい。
というわけで、今回は奥行の推論の応用編として、リアルタイムで介入している対象者の問題解決にも役に立つ方法について解説していく。
奥行の理論の振り返り
前回のブログにおいて奥行の理論の説明に記号と数式を用いて行ったが、まずはそれらを振り返ろう。
以下は前回も提示した表だ。
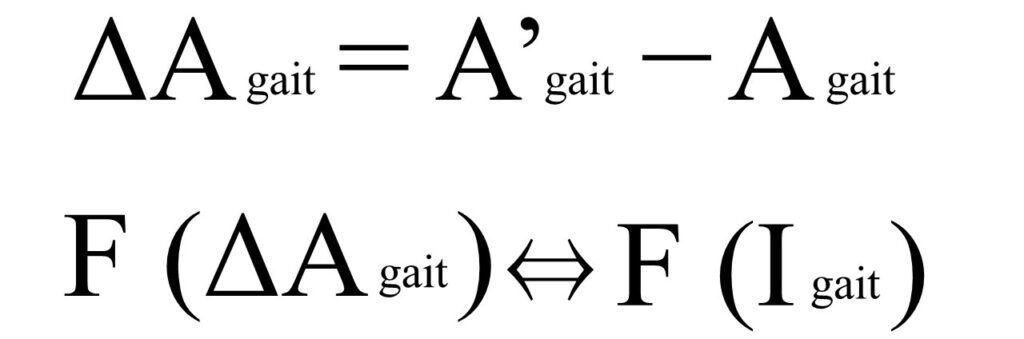
これらのように、時間軸の異なる対象者の状態を比較し、その差異と予測される介入効果とを比較し、対象者の課題について検討するものであった。
言い方を変えると、ある対象者に介入した結果から検討するものであるため、この方法では介入後でないと奥行の理論が成立しない。
こういった問題についての解決策として、奥行の推論の応用方法について説明する。
奥行の推論の応用方法 逆算思考
奥行の推論の応用編を概要は以下になる。
望ましい介入後の対象者の状態を想定し、そこから逆算して介入方法を考えるための推論方法
皆さんはある対象者の担当になった場合に、どのようにして介入プログラムを立てるだろうか?
当たり前のことだが、評価を行い、対象者の状態を把握した上での話にはなるが、大きく分けるとボトムアップ式とトップダウン式に分けられると思う。
ボトムアップ式は、評価により介入の可変可能性の高い部分を見極め、それを基に組み立てていく方法であり、より現実的なプログラムの立て方になると思う。できそうなスモールゴールを設定し、それをクリアすると次のスモールゴールを設定するといったところだ。
〇〇ができれば△△のような、ステップアップ式のプログラムがそれに当たる。
※例:平行棒内歩行 ⇒ 歩行器歩行 ⇒ 杖歩行 ⇒ 独歩
対してトップダウン式は、評価により現実的な可能性を引きつつも、未確定な部分も踏まえて、対象者のあるべき姿、理想的な姿を基に介入プログラムを立てる方法となる。
どちらの方法も評価をしっかりと行っていれば問題ないとは思うが、私はトップダウン式の方法が望ましいのではないかと考えている。
その理由として、ボトムアップ式では目標を達成するのに無駄なステップを踏む可能性が高いことや、対象者の機能改善に依存するため、改善のポテンシャルがあるのにも関わらず、そこを目指せなくなるのではないか考えている。
これはあくまで私の持論であるため、異論反論は受け付けるが、私の経験則上ではトップダウン式に軍配が上がる.
ただ、このトップダウン式については、現在の対象者の状態がどのくらい良くなりそうか、といった予測の精度が重要になるため、ある程度の経験則は必要であることを付け加えておく.
また、このトップダウン式を有効活用するのであれば、現在の対象者の状態を理想的な対象者の状態に近づけるための介入手段の立案が求められる。この際に必要なのが、逆算思考力である。
この逆算思考力に関して、文字通り理想の状態から逆算する力ではあるが、新人や若手のスタッフを教育してたとしても、身につけることが極めて難しい力であると感じている.
ベテランになればある程度自然と身についてくる(身についていないものの方が多いが)が臨床経験の乏しい新人や若手には引き出しが少ないため、どのようにして逆算をしていけばよいかがわからないはずだ。そんな新人や若手の逆算思考力向上に役立つのが奥行の推論の応用編である.
という訳で、次項からは逆算思考力を鍛えるための奥行の推論応用編の中身について解説する。
奥行の推論 応用編について
まず始めに、各種評価を行う。この部分については、通常の理学療法プログラムと同様である。
次に、各種評価結果や本人の意向を基に、対象者のあるべき姿を理想的な姿を設定するが、これをA+と表記する。右上の“+”が理想的な状態を意味する。
この対象者のあるべき姿および理想的な姿であるが、できれば一番高い目標から順々に下げていき、何とか届きそうなレベルに設定することが望ましい。達成可能かどうかわからないレベルだ。
次に、その理想的な状態と現在の状態との差について考えるが、一旦これをΔA+とする。このΔA+の因子、つまりF(ΔA+)について評価の内容から考察する。
最後に、このF(ΔA+)に対する介入方法(I)を考えるといった流れになる。
またこのIについても、前回のブログと同様に内在する因子”F(I)”とF(ΔA+)との関係性から考慮する必要がある。
上と同様ではあるが、一連の関係性を以下に示す。
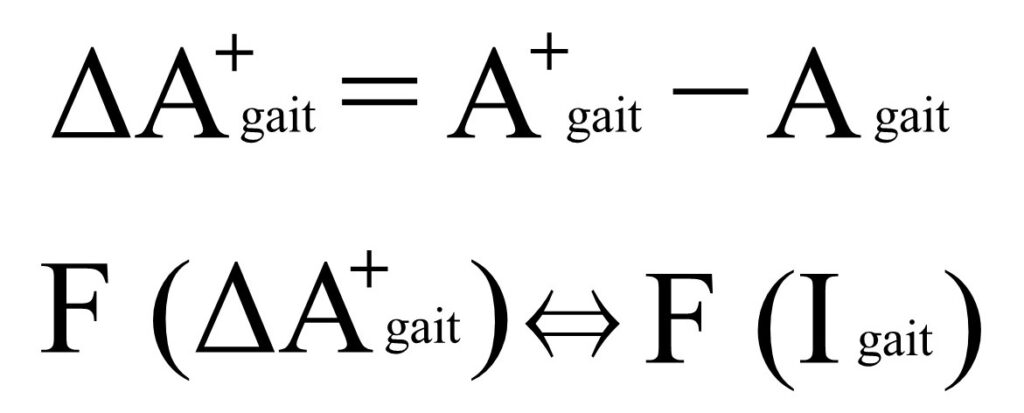
それでは次に、具体例で説明していく。
左下肢の骨折にて免荷期間があり、いざ荷重開始となったものの、いざ歩行すると左立脚時に膝折れが生じていた。
理学療法評価の結果、左膝関節伸展筋力低下と左大腿周径の小さくなっており、廃用性の筋委縮による左膝関節伸展筋力低下によって、歩行時に膝折れが起こっているものと解釈し、膝関節伸展筋力が改善することにより、膝折れが消失するのではないかと推測した。
この状況を数式にし、記号が指す意味を加えると以下になる。

さて、以上のみであればあえて数式にする必要はないだろう。
今回のテーマである奥行の推論の本質は次にある。
奥行の推論の応用 逆算思考力を鍛える
今回説明している奥行の推論の応用編は、理想的な状態と現状との差を可視化するところから始まるが、これについてはあくまで推測の域をでない所に注意する必要がある。
それに対して奥行の推論にて介入手段を考え実行した場合、ある一定期間経つと、実際にどのようになったのか。つまり、介入の結果が返ってくる。これは推測ではなく事実となる。
前回の基礎編において、実際に介入した結果の対象者の姿はA’と表記すると説明したが、今回の応用編で推測したA+と実際の結果のA’を比較することにより、推測と事実の差異を抽出することができる。つまりは以下になる。
自身の推測差異=(A’-A+)
この推測差異を深く考察することによって、自身の推測の精度を上げることが可能となる。この予測精度自体が、逆算思考力の結果に他ならない。
言わば、奥行の推論を駆使することによって、逆算思考力が自然と身についていく。それが奥行の推論の持つ力そのものと言える。
また、推測と事実の比較に関しては、他の項目についても同様のことが可能となる。
例えばΔA+に基づいて介入(I)を行い、結果としてΔA’という結果が得られたということであるため、介入による効果の予測についても検証ができることになる。つまりF(I)についての理解が深まることを指す。
ΔA+を歩行時の膝折れについて膝関節伸展筋力低下をF(ΔA+)と仮定し、それを改善するためにスクワットを介入として選択したという。
このスクワットには膝関節伸展筋力改善というF(I)があると見越しての推論だったが、実際の介入の結果、膝折れが消失し正常歩行に近づいた状態(A’)となった。
この際の介入前後の状態の差(ΔA’)は歩行時の膝折れであるため、F(I)には膝関節伸展筋力改善という因子が含まれていると考えられる。このプロセスによって、スクワットへの理解が深まっていくというわけだ。
逆にスクワットで改善しなかった場合は、F(I)に膝関節伸展筋力改善という因子が含まれていないか、もしくはF(ΔA+)自体が異なっていた可能性が考えらえる。結果的に予測が外れたとしてもスクワットの理解を深める結果に繋がる。
ただ単に何も考えずにスクワットを行うと、膝折れに対してスクワットは効果がないと結論付けて終わってしまうので、理解が深まったとは言えないだろう。
要は、事前に推測した状態と実際の結果を比較することにより、推論精度の向上と他の因子の可能性の抽出が可能になるわけである。
言わば運動学習でいう、教師あり学習と教師なし学習の違いと同じことだろう。
まとめ
「もっと考えよう!」
耳にタコができるほど言われたことがあるかもしれないし、言ったこともあるかもしれない。
ただ気を付けないといけないのは、この”もっと”という概念には無限の幅が存在する。無限の幅というのは一見自由な発想が可能となりそうだが、幅が広すぎてしまうと思考が無秩序になってしまうため、逆に不自由な推論になってしまう。
むしろ、適切な推論の幅を持たせたうえで、そこから生まれる推論の可能性を可視化することによって、思考の幅が広がっていくと私は考えている。
そういった観念において、この奥行の推論は、数式と記号を用いて推論の幅を持たせ、内容を可視化することにより、文字通り推論に奥行を持たせる良いツールである思う。
臨床推論シリーズについては、私の普段の臨床推論の方法を言語化しているものではあるものではあるが、いまいち自分自身でも上手く言語化できていないことから、読者の皆様も意味がわからない所もあるだろう。
ただ知識を教示するのみよりも、こういった形でアウトプットすることによって、私自身の思考の整理にも繋がるため、わかりにくさはご容赦頂きたい。むしろ質問や意見を頂けると、かなり助かるのでよろしくお願いしたい次第である。
という訳で今回は、臨床推論シリーズの中における、奥行の推論の応用編として逆算思考力の重要性とそれを実行するためのツールについて概説した。
特に急性期に関わる人間は、この逆算思考力が必須であると考えているが、なかなか体系的に学ぶことも少なく、悩む人も多いはずだ。
そんな人にとって、この奥行の推論の応用編が役に立つことになれば幸いである。
次回は、奥行の理論とは外れるが、ちょいちょい登場しているF(因子)についての臨床応用方法について説明したいと思う。
この”F”を頭の中で整理できていると、より臨床推論能力が向上すると考えるため、気になった方は、次回もチェックして頂きたい。
それでは今回はこの辺で。
”まじで逆算思考力って大事!これは声を大にして言える”
(´-`).。oO








コメント